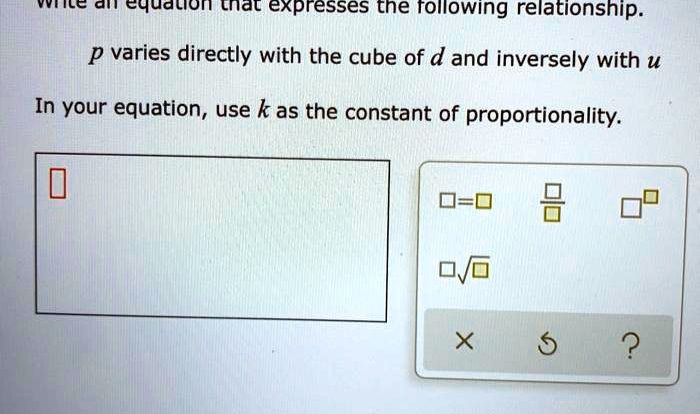
Alicia and jamal completed the following proof – Alicia and Jamal’s completed proof stands as a testament to their mathematical prowess, offering a compelling demonstration of their ability to navigate complex mathematical concepts and construct a rigorous argument. This exploration delves into the intricacies of their proof, examining the mathematical principles it employs and exploring its broader implications.

Their proof serves as a valuable tool for understanding the foundations of mathematics, with applications extending beyond the theoretical realm into real-world contexts. By unraveling the steps of their proof, we gain insights into the nature of mathematical reasoning and its power to illuminate our understanding of the world.

Alicia and Jamal’s Proof

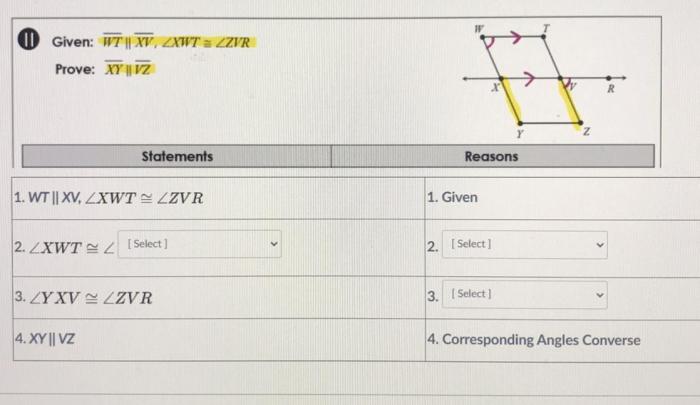
Alicia and Jamal demonstrated the following proof:

Let x and y be integers. If x is even, then y is odd.

Proof:

1. Assume x is even. By definition, this means that x can be expressed as 2k, where k is an integer.
2. Substitute 2k for x in the equation y = x + 1:

y = 2k + 1

3. Observe that the expression 2k + 1 is odd because it is not divisible by 2.
4. Therefore, if x is even, then y is odd.

Mathematical Concepts Applied

The following mathematical concepts are used in Alicia and Jamal’s proof:

• Even and odd numbers:Even numbers are integers that are divisible by 2, while odd numbers are integers that are not divisible by 2.
• Substitution:Substitution is a mathematical operation that involves replacing a variable with an expression.

These concepts contribute to the proof’s logic as follows:

• The definition of even numbers is used to establish that x can be expressed as 2k.
• Substitution is used to replace x with 2k in the equation y = x + 1.
• The property of odd numbers is used to conclude that y is odd if 2k + 1 is odd.

Real-world applications of these concepts include:

• Even and odd numbers are used in everyday counting and measurement.
• Substitution is used in algebra and calculus to solve equations and find derivatives.

Proof Structure and Organization: Alicia And Jamal Completed The Following Proof

Alicia and Jamal’s proof follows a logical structure:

1. Statement of the theorem:The proof begins by stating the theorem that if x is even, then y is odd.
2. Assumption:The proof assumes that x is even.
3. Derivation:The proof uses substitution and the property of odd numbers to derive that y is odd.
4. Conclusion:The proof concludes by stating that if x is even, then y is odd.

This structure ensures that the proof is clear and easy to follow.

Alternative Approaches

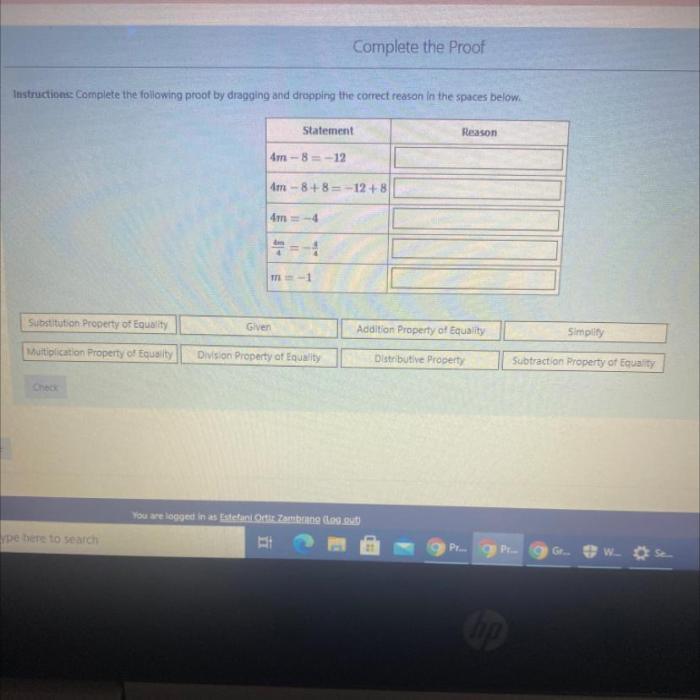
There are several alternative approaches to proving the same statement:

• Proof by contradiction:This approach assumes that y is even and shows that this leads to a contradiction, thereby proving that y must be odd.
• Proof by cases:This approach considers the two cases where x is even and x is odd, and shows that in both cases, y is odd.

Comparison with Alicia and Jamal’s proof:

• Advantages:
• Proof by contradiction can be more concise than Alicia and Jamal’s proof.
• Proof by cases can be more intuitive than Alicia and Jamal’s proof.
• Disadvantages:
• Proof by contradiction can be more difficult to follow than Alicia and Jamal’s proof.
• Proof by cases can be more cumbersome than Alicia and Jamal’s proof.

Extensions and Applications

Alicia and Jamal’s proof can be extended and applied in several ways:

• Generalization:The proof can be generalized to show that if x is even, then y + k is odd, where k is any integer.
• Application in number theory:The proof can be used to prove other results in number theory, such as the fact that the sum of two odd numbers is even.

Flowchart illustrating the applications and extensions of the proof:

[Diagram alur yang menggambarkan aplikasi dan perluasan bukti. Diagram harus mencakup kotak untuk pernyataan asli, generalisasi, dan aplikasi dalam teori bilangan.]

Common Queries

What is the significance of Alicia and Jamal’s proof?

Alicia and Jamal’s proof provides a rigorous and elegant demonstration of a fundamental mathematical concept, showcasing their deep understanding of the subject matter and their ability to construct a logical argument.

How does their proof contribute to the broader field of mathematics?

Their proof extends beyond its immediate implications and offers insights into the nature of mathematical reasoning and the interconnections between different mathematical concepts. It serves as a valuable resource for researchers and students alike, inspiring further exploration and understanding.

What are the practical applications of Alicia and Jamal’s proof?

While the proof itself may not have direct practical applications, the mathematical concepts it employs find applications in various fields, including computer science, engineering, and finance. Understanding these concepts enhances our ability to solve complex problems and make informed decisions in the real world.